Philopure : Pensée mathématique ; vision, division, illusion. Commentaire de Spengler, « Le déclin de l’occident »

Pour une lecture préliminaire vous trouverez le texte à la fin de ce commentaire.

La vision que développe Spengler dans Le déclin de l’occident est celle de l’Homme à travers les sociétés humaines comparées à des organismes vivants. C’est-à-dire que les civilisations naissent dans un état informe avec un grand avenir, elles murissent jusqu’à leur apogée après quoi elles vieillissent et finissent par mourir. Dans ce processus de développement, l’occident se situe à la fin de sa vie, c’est une civilisation décadente. Il n’a d’ailleurs aucune sympathie pour les nazis qui n’est qu’un signe prégnant de ce déclin. De la même manière, il est possible de voir dans la science un déclin, une limite qui est sur le point d’être atteinte, qui est là aussi le reflet et un facteur du déclin de notre civilisation. C’est ce que nous allons examiner dans cet extrait de la première partie du Déclin de l’occident, au paragraphe cinq du premier chapitre.
Ce texte porte sur la mathématique. Pour Spengler la mathématique moderne est une vision du monde dont l’illusion est de croire qu’elle porte sur le général, qu’elle est vraie hors de notre temps, de notre culture. Nos habitudes de pensée sont non seulement la cause de cette erreur mais aussi la difficulté à dépasser pour soutenir cette thèse. L’illusion mathématique si ce n’est scientifique est de juger négativement une autre vision ou pensée à partir des attentes et des besoins spécifique à sa propre culture. Cette dernière est prisonnière d’une vision qui limite son entendement, sa capacité de compréhension.
L’enjeu est donc de libérer la mathématique moderne de sa confusion ou de son désintérêt pour la dimension culturelle, c’est à dire de son illusion. Ce dépassement représente la naissance d’une nouvelle vision du monde, d’une nouvelle vision de la mathématique affranchie de ce carcan, de ce manque de souplesse ou encore de perméabilité.
Pour ce faire, Spengler commence par une comparaison rétrospective entre les visions du monde de la mathématique antique et moderne des lignes 1 à 11 en montrant en quoi notre mathématique et sa vision est limitée au moins autant que nous le pensons aujourd’hui de celle de la mathématique antique. Nous verrons en quoi pour la culture antique, notre vision mathématique n’avait et ne pouvais pas avoir de valeur, de sens ou même de réalité.
Il va ensuite montrer qu’il n’y a pas de hiérarchisation des visions mathématiques. L’une n’est pas supérieure à l’autre mais simplement différente puisque produit d’une culture différente. Cette seconde partie des lignes 12 à 18 permettra de démêler cette confusion des habitudes de pensée de la mathématique moderne, notamment en montrant que cette même erreur a été faite par les antiques. La distinction qui sera faite portera sur la mathématique antique en tant qu’elle est une représentation du monde réel et sensible alors que la mathématique moderne n’est pas une vision du réel ainsi pensé mais une abstraction par idée et concept.
Le troisième temps de cet extrait se rapprochera de son enjeu, des lignes 18 à 28. En tant que produit de la culture, il n’y a pas une mathématique mais « des » mathématiques. Cette partie démontrera que notre erreur a déjà eu des conséquences certes inobservables mais pas moins efficientes puisque notamment, elles sont ce qui participe de notre déclin. Il nous est donné de les percevoir en observant le déclin de la culture grecque qui procéda d’une erreur que nous sommes nous-mêmes en train de faire. De ce fait, il faut étendre notre champs de vision à d’autres méthodes et visions du réel, et pas simplement les délaisser après s’être illusionné de sa vérité mathématique bien huilée. La méthode de notre « vraie » mathématique ne fait que borner la pensée empêchant ainsi l’apparition ou la naissance d’une vision du monde ou du réel nouvelle et d’une certaine manière plus adéquate.

Le texte commence ainsi par présenter la caractéristique principale de l’Homme et de la culture « antique ». Nous pouvons remarquer qu’il est déjà question de vision dans l’expression d’ « être éveillé » qui fait appelle à l’ouverture du regard. Cette ouverture a donné, a produit « tout ce qui est né » de ce que nous connaissons aujourd’hui de la civilisation grecque. Cette naissance de la culture antique s’est faite à partir d’une considération du monde, du « réel » tel qu’il leur apparaissait comme vrai et dont la caractéristique essentielle ou pierre de touche fut la « limite plastique » (ligne 2). Cela signifie que le savoir est celui de la matière. La matière ou le sensible est ce qui fait sens à l’intelligence du savant antique. C’est pourquoi la science de l’antiquité est la géométrie. Il est ici question de géométrie car la « plastique » renvoi non seulement au sensible, au matériau mais aussi à la forme. De ce fait, le savoir ou science de la forme est la géométrie. Il n’y a de science que de ce qui relève de la géométrie, de la forme et de fait, de ce qui peut se « dessiner ». La géométrie est la science qui représente la forme matérielle par le dessin d’une part, et le « nombre » d’autre part qui en est sa proportion, sa cohérence, son harmonie. Le terme « nombre » est ainsi mis entre guillemets pour insister sur le fait qu’il n’est pas une abstraction de l’esprit, un concept mais une représentation de la réalité matérielle. Il n’y a de science et de méthode de connaissance que de ce qui est ou existe matériellement.
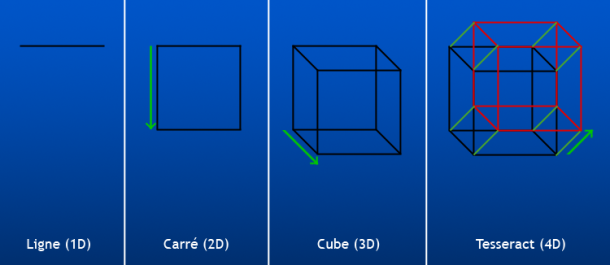
Pour approfondir et développer davantage cette caractéristique antique de la conception de la science, Spengler fait référence à Platon, Archytas et Eudoxe. Platon était philosophe et son grand intérêt pour la science telle qu’elle vient d’être présentée est bien connue et était même clairement visible à l’entrée de l’Académie qu’il créa. Il y était inscrit « Que nul n’entre s’il n’est d’abord géomètre ». Pour Platon, la connaissance ou la formation de l’esprit commençait par la géométrie. Autrement dit la science est d’abord celle de la matière et de ses formes. Eudoxe était lui aussi géomètre ainsi qu’astronome, médecin et philosophe. Quant à Archytas, il était mathématicien, homme d’état et philosophe mais surtout, il fut le professeur d’Eudoxe et un intime de Platon. Tous trois sont donc très liés et parlent de « nombres-plans et de nombres-corps » (ligne 3). Les « nombres-plans » correspondent à des représentations en deux dimensions, des surfaces c’est à dire la « 2e puissance ». Pour l’illustrer, nous pouvons nous référer au carré, qui est une surface en deux dimensions, sur un seul plan et dont la puissance est deux. Pour calculer l’aire d’un carré, il faut élever la longueur d’un côté au carré ou encore à la puissance deux. Les « nombres-corps » correspondent à des représentation à trois dimensions, des volumes c’est-à-dire la « 3e puissance ». Pour l’illustrer, nous pouvons nous référer au cube, qui possède bien quant à lui trois dimensions et dont la puissance est trois. Pour calculer le volume d’un cube, il faut élevé la longueur d’un côté au cube ou encore à la puissance trois.
Nous voyons donc bien que la science porte sur la forme de la matière, c’est pourquoi nous parlons de science par la géométrie à l’antiquité bien plus que de science par la mathématique. La mathématique n’est pas une science en soi et abstraite, mais fait partie de la science qu’est la géométrie en tant qu’outil ou méthode. C’est pourquoi nous dit Spengler une « dimension supérieure à ces nombres » n’a pas lieu d’être, « n’existe pas » (ligne 4). Cette réalité n’a pas de topos, au sens de réalité matérielle. Le réalité scientifique antique est la géométrie, la forme matérielle et donc le réel tel qu’il nous est naturellement donné de l’observer. « Une dimension supérieure à ces nombres » par exemple une quatrième dimension, « Une 4e puissance » ne se trouve pas dans la nature telle qu’elle nous est donnée, elle ne se trouve pas dans la plastique, dans la forme matérielle naturelle. Et puisque c’est dans cette forme matérielle que la science de la géométrie trouve sa pierre de touche, ce qui constitue son « sentiment fondamental » (ligne 5), la science portant sur une dimension qui n’a pas de réalité, qui n’est pas matérielle ne peut en aucune façon être comprise. Cette incapacité peut être observée dans la méthode même de compréhension qui a directement trait à ce « sentiment fondamental ». Car pour comprendre, le géomètre commence par tracer, par dessiner. Or une quatrième dimension ne se trace pas, ne se dessine pas et ne se représente pas plastiquement. Il y a un « non-sens » « à ce mot » de quatrième dimension par incompatibilité de ce dont à quoi elle renvoi et qui n’a rien à voir avec une représentation de la forme matérielle entendu pour le savant antique comme le réel.
Nous venons ainsi de voir ce par quoi la vision savante de l’antiquité était caractérisée, c’est-à-dire la forme matérielle. Spengler développe davantage sa critique rétrospective de notre science en s’appuyant sur deux « expressions » (lignes 6 et 7), deux méthodes de notre science. Déjà, la science qui a supplanté celle des grecs n’est plus de l’ordre de la géométrie mais de la mathématique. C’est pourquoi les exemples empruntés sont cette fois d’ordre mathématique et non pas géométrique. En outre, Spengler l’indique à la ligne 7 en disant que c’est ce « qui apparaît constamment dans nos formules ». La base n’est donc plus la forme matérielle mais le nombre mathématique lui-même. La première expression qu’il mentionne est « du type e-^ix ». Ce que nous pouvons remarquer d’intéressant par rapport à ce que nous venons de développer concernant la vision antique du savant est contenu dans les termes de la puissance. Il y a deux choses. D’une part une puissance ne peut être en aucune façon comprise comme négative dans le contexte antique. Puisque celle-ci est l’expression d’une dimension, il est impossible de se représenter une dimension de la réalité qui soit négative. Par exemple, la négation de la seconde dimension n’a pas de signification au sens ou elle s’observe en tant que « positive » dans la réalité des formes géométriques de manière nécessaire, c’est-à-dire qu’elle n’est pas et ne peut être autrement. Il n’est de fait pas utile pour l’antique de la penser autrement. D’autre part et cela renchérit avec ce qui vient d’être expliqué, il s’agit dans l’expression « e^-ix » de la puissance d’un nombre imaginaire « i », c’est-à-dire qui n’existe pas. Pour le grec antique le résultat d’une puissance ou d’une racine carré est un nombre que l’on peut trouver sur une règle, c’est un nombre qui existe. Comment penser pour un grec antique la représentation d’une dimension qui n’existe pas et dont la représentation est imaginaire ? C’est tout à fait impossible, il ne peut en aucune façon se la représenter et donc la comprendre.
La seconde expression, 5^1/2 présente un problème du même ordre. La question que se poserai l’antique est de se demander comment une dimension peut-être divisée. Par exemple, le carré est entier en tant qu’il correspond à la deuxième dimension. En vain et tant bien même que le grec antique couperai son carré dessiné en deux par égales en suivant une diagonale, il se trouverait toujours dans la seconde dimension, c’est-à-dire que ses deux moitiés se trouveraient nécessairement sur un plan. Une fraction de dimension n’a donc pas de réalité géométrique puisqu’elle ne correspond à aucun tracé de formes.
Nous sommes de ce fait en mesure de comprendre en quoi cette science mathématique illustrée par ces deux formules « leur eussent parues tout à fait absurdes. » (ligne 8). Et concernant la deuxième expression 5^1/2, Spengler ajoute encore quelque chose à sa démarche de critique rétrospective en faisant référence à Nicolas Oresme à la ligne 8. Spengler souligne ici, outre la limite de notre science mathématique par la vision antique le fait que cette science que nous pensons comme nouvelle ou évoluée n’est historiquement pas récente et novatrice. Non seulement notre supériorité scientifique ne fait pas sens pour la vision antique, mais elle ne vient pas de nous, elle ne nous appartient pas directement mais nous n’en tenons qu’un aboutissant. C’est-à-dire que cette expression 5^1/2 qui est une base de la mathématique actuelle et dont on se réclame et se sur-estime vis-à-vis d’une autre vision scientifique antérieure ne vient pas de nous, ni de nos contemporains. Cette base vient du Moyen-Âge, au XIVe siècle, elle est donc très ancienne. Notre prétention de supériorité ne tient pas pour la vision grecque mais aussi dans la construction même de cette mathématique considérée dans sa dimension historique. Ceci est une mention qui donne donc encore davantage de poids à la critique qu’il développe.
Il poursuit en se référent cette fois à Euclide à la ligne 9, grand mathématicien de l’antiquité grecque. Spengler présente la définition euclidienne des « côtés » en tant que « facteurs d’un produit » (ligne 9). Pour le comprendre, reprenons l’exemple du carré qui représente la seconde dimension ou 2e puissance. Pour calculer une surface, une aire nous avons dit que nous élevions la longueur d’un coté au carré, à la puissance deux. Or une puissance est une multiplication d’un nombre par lui-même, c’est-à-dire un produit. C’est pourquoi Euclide appelle « côtés » les « facteurs d’un produit », ce qui est susceptible de représenter une surface par sa multiplication. Les côtés ne sont donc pas des segments abstraits mais des facteurs de produit, des éléments permettant une représentation géométrique du réel matériel.
Suite à cette définition, il nous présente la méthode d’Euclide qui consiste à « compter par fractions ». Cette méthode est « définies » et « s’entend », ou encore prend sens pour la compréhension antique « en cherchant le rapport du nombre entier entre deux ligne » (ligne 10). Cela signifie que pour Euclide et ses contemporains une fraction représente un découpage en morceaux égaux d’un segment, d’une longueur. Par exemple, la fraction 3/2 ne représentait pas une division, entendue une division de chiffre mais une comparaison. L’antique tracerai une « ligne » de trois centimètre par exemple d’un point A à un point B. Il placerai un point C au milieu de AB et dirait que AB est deux fois plus long que AC, ce qui donnerai la signification de la division par deux d’une ligne de trois centimètres, c’est-à-dire 3/2. Remarquons ici qu’il n’est pas question de segment dans le texte ni même de droite mais de « ligne ». La ligne est ce que nous pouvons observer dans la réalité des formes matérielles alors que le segment ou la droite font parties des abstractions mathématiques qui comme nous venons de le voir ne font pas sens dans la science d’ordre géométrique de l’antique. Et cet exemple de la fraction et de sa compréhension antique permet cette fois la critique d’une autre de nos grandes bases de la mathématique moderne, celle du « zéro » (ligne 11). En géométrie, il est tout simplement « impossible », inimaginable de comparer une longueur avec rien, une longueur nulle ou un point. Cela ne donne rien, cela ne produit pas de sens pour l’antique entendu aussi si l’on reprend notre exemple de 3/2 que AB ne peut pas être zéro fois plus long que AC. Nous voyons même que la formulation d’une telle abstraction est presque impossible en des termes antiques.

Concevoir la quatrième dimension

La critique rétrospective des fondements mêmes de la mathématique actuelle est ici achevée aussi bien sur le plan de la vision que de la méthode. À partir de cette critique des bases mêmes de notre mathématique moderne, Spengler va ainsi montrer que cette incompréhension du savant antique fut une erreur, erreur qu’à notre tour nous commettons. Ceci l’amènera à démontrer qu’il n’y a pas de hiérarchisation entre la mathématique antique et moderne.

C’est pourquoi il commence d’emblée par se défendre de ce qu’il s’attend finalement à entendre en disant « N’allez pas m’objecter » (ligne 12). Par cette formulation rhétorique il prévient par avance ou anticipation qu’il a déjà pensé à ce dont nous pourrions nous-même penser en tant qu’objection de ce qui vient d’être dit. Et ce dont il serait possible de faire appelle est de l’ordre de ce que ce qui est construit, « constituée » (ligne 12) sur cette illusion que nous venons d’expliquer en première partie. Cette construction repose sur cette confusion ou ce manque d’égard de nos « habitudes de pensée » envers des différences de culture qui sont elles-mêmes la base d’une autre science elle aussi différente, entendu que la science est le produit de la culture selon Spengler. Et c’est à partir de cette erreur, en n’ayant un point de vue en surplomb ou dépourvu de rétrospective que nous jugeons la science antique en la désignant comme « degré primitif » (ligne 13). Comme nous l’avons dit, il n’y a pas de hiérarchisation ou encore de gradation en degré dans l’histoire de la science. Il manque la dimension culturelle, ce que Spengler constate en insistant sur l’unicité ou la simplicité de notre considération c’est-à-dire « « la »mathématique en général ». Autrement dit, une science est relative à son contexte ou à son époque pour être comprise telle qu’elle est, sinon nous sommes dans l’erreur de penser qu’il y a gradation. C’est cette idée de lien culturel qu’il développe par la suite.
Il part de nouveau de la culture antique, de la vision du monde, du réel ou du « cadre de l’univers » (lignes 13 et 14) qu’avait cette culture pour produire la science que nous avons analysé en première partie. « Le cadre de l’univers » est le cosmos, c’est-à-dire une totalité parfaite, harmonieuse et organisée par dieu. De ce fait la géométrie est ce qui permet à l’Homme antique de comprendre cette création, cette œuvre divine. La géométrie donne un sens pour les Hommes à cette totalité divine et en fait partie. C’est pourquoi leur mathématique « est quelque chose d’achevé » (ligne 15). Puisque leur mathématique sont appliquées à la géométrie qui elle-même porte sur la réalité matérielle considérée comme un tout divin donc parfait, harmonieux et organisé, rien ne peut leur échapper, elle peut tout saisir, tout comprendre du monde matériel, elle est achevée. La géométrie fait partie du monde, un monde qui leur est donné par dieu. Toutes leurs notations, par exemples leurs puissances qui se limitaient à trois leurs suffisaient pour tout décrire, pour tout comprendre, il n’avaient besoin de rien de plus.
Pour nous qui ne possédons pas une telle considération du monde, l’univers ne se réduit pas à sa dimension matérielle. Il n’y a pas une réalité mais des réalités, des possibles. Par exemple, nous admettons l’existence d’une quatrième dimension. Elle ne fait pas partie de notre réalité matérielle mais existe de manière abstraite, sous forme d’idée, de concept. De ce fait et puisque les possibles sont infinis, la mathématique est « imparfaite » (ligne 15). Mais cela ne dépend que de notre culture, de ce qui a été cultivé à partir de la science d’autres époques, par exemple l’abstraction par le nombre « déjà connue de Nicolas Oresme au XIVe siècle ». Cette mention indique en outre qu’il n’y a non seulement pas de degré distinct, c’est-à-dire primitif et un autre évolué mais qu’il y a mélange et superposition des visions et des méthodes. Il ne faut pas dire que la vision antique était dans le faux, ou à un degré inférieur de vérité par rapport à notre vision actuelle. Cette considération ne tient pas. Pour bien comprendre une pensée mathématique, il faut aussi considérer la culture dont elle est le produit.
Et c’est aussi l’erreur que les scientifiques antiques ont fait à l’égard des mathématiques « de Babylone et de l’Inde » (ligne 16). Cette critique rétrospective de nos considérations actuelles de la mathématique devient ici une critique même de la considération du savant antique. C’est-à-dire que notre erreur fut aussi celle de l’antique dans ses propres considérations de notre mathématique apparaissant à son époque dans la culture orientale. Et c’est ce par quoi Spengler entend bien nous en faire tirer une leçon, un enseignement pour nous conduire à l’enjeu de ce texte. Car la mathématique en tant qu’abstraction par idée et concept que nous nous approprions en la qualifiant de moderne est en fait très ancienne, ce que nous avons déjà commencé à voir avec Nicolas Oresme au Moyen-Âge. Mais cette référence à Babylone et l’Inde est encore plus ancienne et plus directement lié à l’époque antique grecque puisque « maint penseur grec le savait » (ligne 17 et 18). Et les savants grecs savaient que ces deux autres cultures avaient découvert ce que nous pensons aujourd’hui tenir de notre propre progrès, de notre propre effort. Ces découvertes dites modernes ne nous appartiennent pas et l’erreur que nous faisons aujourd’hui n’est pas nouvelle. Elle date de l’antiquité même, de ce que nous considérons, rappelons-le, à tord comme un « degré primitif ».
En premier exemple les Babyloniens, par leurs besoins de la vie économique et sociale ont provoqué l’utilisation des mathématiques. Ils ont écrit les première équations, c’est-à-dire des égalités mathématiques avec un inconnu. Il s’agit de l’invention d’une mathématique abstraite telle que nous la connaissons aujourd’hui et qui n’est pas ce que faisait la géométrie qui s’attachait directement à la réalité de la matière et de sa forme.
Quant aux Indiens, ils ont par exemple fait partie des culture à avoir maîtrisé le zéro, les nombres négatifs ou encore les fonctions trigonométriques. Ces bases de nos mathématiques ne nous sont parvenues en Europe que bien plus tard après avoir trouvé un échos en Chine et dans les mathématiques arabes. Il aura donc fallu à l’occident une certaine ouverture d’esprit, une certaine ouverture culturelle pour recevoir cette mathématique nouvelle, celle de l’orient. C’est cette écoute ou capacité de compréhension que les grecs antiques n’ont pas pu avoir. Ils étaient finalement comme emprisonnés dans le carcan de leur science géométrique bien huilée, finit, parfaite, bien encrée dans leur vision culturelle du monde. Autrement dit, leur vision du monde leur avait donné la mathématique de la géométrie mais ayant été considérée comme complète et suffisante, elle s’avéra en réalité fermée, sourde à toute autre vision, à toute autre influence culturelle et de fait à un niveau d’abstraction qui, leur faisant défaut, a contribué au déclin de leur civilisation. Ils n’ont pas su se créer les besoin culturels nécessaires à sa réception. Le niveau d’abstraction de la mathématique moderne ignoré, ils ont été dépassé par ceux qui avaient besoin de cette abstraction pour répondre à des problèmes bien plus compliqués que ceux que pouvaient poser la géométrie antique.
Ainsi, le comportement qu’on eut les savants antiques à l’égard des mathématiques modernes est ce qui a contribué à leur déclin, leur dépassement. Et nous pouvons voir rétrospectivement que c’est ce même comportement que nous adoptons aujourd’hui. Pour le scientifique actuelle, la mathématique est telle qu’il la conçoit et pas autrement, par exemple nous dit Spengler, elle est « imparfaite ». Et si on lui présentait une vision différente, alors ils ne pourrait s’y ouvrir, croyant avoir la primauté de grandes découvertes, de méthodes infaillibles qui est le reflet prégnant de ce que qu’a pu être la considération antique de nos mathématiques à ses début. C’est pour cela que Spengler insiste sur le fait que la mathématique « n’est imparfaite que pour nous ». Elle est imparfaite pour nous qui vivons dans une certaine époque, une certaine culture dont les besoin on produit cette considération. Mais étendre cette vision au monde, à l’histoire ou encore à d’autres cultures en la présentant comme seule vraie, comme fleuron du progrès à l’instar des grecs pensant qu’ils n’avaient besoin de rien d’autre que leur mathématique fondée sur la géométrie, alors c’est être, nous dit Spengler dans « l’illusion » (ligne 18). Autrement dit, nous nous trouvons dans l’illusion dès lors que nous considérons qu’il y a une mathématique, « « la » mathématique » (lignes 13 et 18). C’est bien ce que Spengler à l’intention de dire, de démontrer et de pointer du doigt dans ce texte en disant que « nous ne cesserons de le répéter ». Et le fait même de le dire, de prononcer « la mathématique », de le « répéter » contient déjà en soi cette illusion et cela fait aussi partie de nos habitudes de pensée, ce sont là les habitudes de langage.
La mathématique doit donc être aussi comprise comme une culture, avec son système de valeurs et de croyances. Il y a une mathématique du grec antique, une mathématique Babylonienne, Indienne et aussi une mathématique de notre culture. Nous sommes dans l’erreur dès lors que nous faisons sortir notre vision mathématique hors de son champs culturel puisqu’il y a dès cette limite dépassée une incompatibilité culturelle empêchant tout rapport de comparaison, et par là de supériorité. C’est en cela que tient notre illusion pour Spengler.

Nous allons à présent nous diriger vers l’enjeu de la thèse de Spengler c’est-à-dire la naissance d’une nouvelle mathématique, le dépassement de notre vision scientifique. Il sera donc à nouveau question des limites que pose notre vision mathématique, ce qui constituera à la fois un facteur d’empêchement de naissance d’une nouvelle mathématique mais aussi un signe supplémentaire de notre déclin. Ce que nous empêchons de naître et que nous ne sommes pas en mesure d’assumer ou de comprendre finira par nous dépasser comme ce fut le cas pour les grecs antiques.

Spengler commence par éclaircir cette confusion, source d’illusion mathématique. Il définit la « pensée mathématique » et à travers celle-ci une pensée « scientifique ». De fait, la pensée mathématique est « juste » et « convaincante » (ligne 18), ce que ces penseurs ont pour habitude de considérer comme « logiquement nécessaire » (ligne 19 et 20), c’est-à-dire ce qui est vrai uniquement dans le contexte de leur culture. Cette démonstration par la pensée mathématique ne suffit pas à elle seule, elle doit aussi répondre à un contexte culturel donné, y être corrélé. C’est-à-dire qu’elle doit être logiquement nécessaire en soi mais aussi en rapport avec les éléments du contexte intellectuel, de la culture. Et cette dimension culturel selon Spengler se traduit par un « sentiment de la vie de l’auteur » (ligne 20). Bien que ce dont sur quoi porte la pensée de l’auteur soit abstrait (des concepts ou idées tels que la quatrième dimension, les nombres imaginaires ou encore le zéro), sa pensée elle-même n’est pas abstraite au sens où d’une certaine manière elle reste encore rattachée à la réalité matérielle de son temps, elle s’encre nécessairement dans sa culture. Cette pensée est un accord avec les données de la culture, c’est-à-dire avec sa vie. Sa « vie » ou son vécu est l’enseignement qu’il a reçu. Le penseur est donc l’héritier d’un processus interculturel complexe. Avec le fruit de cet héritage, il doit « répondre » à une intuition, un « sentiment » qu’il repère ou décèle en vivant dans cette culture qu’est la sienne. Nous pouvons remarquer qu’il ne s’agit pas non plus de répondre vraiment à des besoins, ce qui relèverai plus des sciences physiques ou encore biologiques mais à ce qui relève de l’abstraction. C’est pour cela qu’il répond à un « sentiment », quelque chose d’abstrait, d’indéfini. Puisque le penseur de la mathématique moderne travail sur des idées et des concepts abstraits détachés de toute réalité matérielle, il ne peut pas vraiment avoir de vision ou de représentation. Il est bien plus question d’intuition. Par exemple c’est par intuition que l’on pense ce que nous appelons l’ « hypercube », un cube à quatre dimension. C’est ce que signifie la notion de « sentiment », une intuition de ce qui est possible mais non réel matériellement dans notre contexte culturel donné, dans lequel nous vivons.
De fait, le vrai pour un penseur mathématique n’est possible que dans ce contexte, celui de sa vie, son temps, sa culture. En dehors de ce contexte, il ne peut y avoir de vrai, c’est « impossible » (ligne 21) puisque de façon rétrospective nous ne pourrions pas nous empêcher de penser avec ce que nous avons appris de notre culture, ce qu’elle a fait de nous ou encore ce qu’elle a produit à travers nous dans le domaine de la science. C’est en ce sens aussi qu’elle est « avortée ». Une pensée mathématique étrangère ne peut pas même prendre forme, ne peut pas naître en tant que produit d’un sentiment, d’une culture, si nous ignorons celle-ci. Autrement dit, la pensée différente de notre culture en dehors de son contexte perd son substrat nourricier et fertile et demeure à l’état d’idée « insensée », dont on ne peut comprendre la raison et finalement ce qui en rend raison, c’est-à-dire sa culture ou le contexte dans lequel notre pensée s’est aventurée ou ingérée. Par là, ce que nous nous plaisons à dire pour flatter notre position culturelle ou « historique », « le mot favori de notre orgueil » est issu de notre position de surplomb finalement fausse et infondée culturellement. Cette erreur, cette « illusion » dans cette façon de voir incorrecte nous conduit à considérer cette pensée d’une époque passée comme « primitive » (ligne 22). En effet, détachée de son contexte historique ou culturel une pensée mathématique ne répond pas au même sentiment ou exigence que l’époque à partir de laquelle on l’a juge. C’est pourquoi elle ne nous paraît pas, peu ou pas assez efficace ce qui nous conduit à la juger inférieure à la nôtre, moins évoluée, plus « primitive ».
Spengler n’enlève rien de la performance de notre mathématique qu’il qualifie même de « chef d’œuvre occidental » (ligne 22) mais cette mathématique doit, pour conserver cette place tout simplement y rester. Car il le répète une fois encore, cette mathématique ou esprit mathématique en tant qu’il pense par cette science n’est « vraie » (ligne 23) qu’en tant que l’esprit ne déborde pas de son temps, de la culture qui l’a produite. C’est-à-dire que sa mathématique n’est « « vraie » en tout cas pour lui seul » (ligne 23).
Car il pourrait se produire l’inverse, ce qui rappelle que ce non-sens marche aussi du côté de la pensée que nous surplomberions envers nous-même. Spengler revient à la vision antique avec Platon qui, avec ce que son temps lui permettait et/ou pouvait être en position de réclamer ne pouvait voir en de pareilles mathématiques, entendu celles de notre « esprit occidental » rien de concevable et d’applicable mais y verrait bien plus « une méthode aberrante et ridicule » (lignes 23 et 24). En effet comment résoudre des problèmes pratiques de géométrie avec des nombre imaginaire, un zéro ou une dimension qui ne représente et ne correspond à rien de la réalité matérielle pour « la « vraie »[…] l’antique mathématique » (ligne 24) portant sur la réalité sensible. Au lieu de s’en « approcher » notre mathématique s’en éloigne au contraire, au point de provoquer de l’étonnement, de l’incompréhension et de l’ironie car elle serait bien plus prise comme une forme de rêverie que comprise comme un « chef d’œuvre ». Cette vision grecque considérant la mathématique moderne aberrante est le reflet de l’erreur qu’ils ont commis et que nous commettons. Il est aussi ridicule et aberrant de juger une autre pensée à partir de ses valeurs culturelles.
A partir de cette erreur que nous aussi avons eu et avons dans nos considérations « des cultures étrangères » (ligne 26), nous pouvons constater qu’il y a de fortes chances si ce n’est qu’ « il est certain » (ligne 24) que nous avons avorté, empêché et « laissé périr » (ligne 25) ce qui aurait pu être l’émergence, l’ «éveil » ou encore la naissance « de grandes pensées », d’autres visions qui auraient eut sens, auraient été vraie pour la culture donnée. Mais notre erreur nous a illusionnée d’orgueil, d’un amour propre aveuglant tel l’artiste trop fier de sa grande « œuvre ». C’est ce qui constitue « les bornes de notre pensée » (ligne 26). Notre pensée est bornée à la méthode de notre mathématique moderne comme la pensée antique l’était de sa géométrie. Et par cette même erreur nous courons tout aussi certainement à notre propre perte, à notre déclin. Car ce que nous empêchons de se construire sera aussi ce qui, comme pour les grecs antiques nous dépassera. Notre vision mathématique moderne nous conduit ainsi à juger toute autre pensée mathématique « fausse, superflues, insensées » (ligne 28), car comme les grecs antique l’on fait, elle est prise en dehors de son contexte qui lui permet cette magnificence, c’est-à-dire en dehors des réponses finalement précise qu’elle donne à son temps et du sens qu’elle produit dans celui-ci. C’est ce que nous faisons et ce qui nous empêche d’ « assimiler » (ligne 27) ces émergences de nouvelles grandes pensées. Si nous les assimilions, nous dépasserions nous-mêmes notre niveau de compréhension. Nous pouvons dire que nous évoluerions. Par là notre culture changerai, elle évoluerai alors que dans cette incapacité due à notre illusion, nous les rejetons dans un état primitif jusqu’à ce qu’elle finisse par se donner les moyens ailleurs de nous surplomber à son tour, nous dépasser et nous laisser périr. En ce cas, il s’agirait d’une révolution, notre pensée mathématique rigide serait révolue. C’est ce que nous avons pu observer avec les grecs antique qui n’ont pas prêté attention aux mathématiques Babyloniennes et Indiennes qui ont trouvé une culture favorable en Europe à leur développement, leur établissement, pour se diffuser et dépasser la science grecque.

Construction de l’hypercube par exposition et superposition de dimensions

Dans la réponse à l’enjeu de ce texte, nous pouvons ainsi trouver deux choses. La première est une réponse, comme une mise en garde à notre égard. Il faut que nous nous soucions de la dimension culturelle. Les choses ne sont pas distinctes. Il n’y a pas d’un côté la science, qui évolue par degré, et de l’autre la culture, qui suit ou change en parallèle. Cette vision est bien plus une illusion et conduit à une rigidité qui bloque ou borne notre évolution ou progrès scientifique. Car les deux niveaux, culturels et scientifiques en réalité se mélangent. La science est un produit de la culture, elle nait pour répondre à des attentes ou des besoins. En cela elle évolue en fonction de ces besoins et de ces attentes. La science fait partie d’un processus et n’est forte de sa pensée que dans le contexte auquel elle répond.
Voici donc la marche à suivre, la bonne pensée ou encore une vision claire qui permet d’affranchir une pensée mathématique des bornes de la culture qui l’a fait naître. Mais ceci nous amène à la seconde chose. Bien que ce texte pose les conditions d’une pensée mathématique ouvertes à l’enrichissement interculturel, c’est-à-dire que bien qu’il se montre positif puisqu’il expose une solution à notre erreur, Spengler montre que malgré tout nous nous trouvons dans un déclin inéluctable.
Malgré qu’il y ait une ouverture possible, nous sommes trop fier et imprégné de notre culture, nous pouvons même dire que nous en sommes prisonnier. De sorte que nous nous dirigeons certainement si ce n’est inéluctablement vers le même sort que celui qu’a connu la pensée mathématique antique grecque et sa culture. Ce texte est par conséquent le triste constat de la fin imminente de ce vieil organisme, notre culture occidentale. Et Spengler pourra être considéré comme faisant partie de « maint penseur » qui « le savait ».

« Tout ce qui est né de l’être éveillé antique n’a donc été élevé au rang de réel que par sa limite plastique. Ce qui ne peut pas se dessiner n’est pas non plus un « nombre ». Platon, Archytas et Eudoxe parlent de nombres-plans et de nombres-corps pour dire 2e et 3e puissances, et il va de soi que le concept de puissance supérieure à ces nombres n’existe pas pour eux. Une 4e puissance serait un non-sens pour le sentiment fondamental qui donne aussitôt à ce mot une étendue à quatre dimension et matérielle. Même une expression du type e^-ix qui apparaît constamment dans nos formules, ou bien simplement l’expression 5^1/2 déjà connue de Nicolas Oresme au XIVe siècle, leur eussent parues tout à fait absurdes. Euclide appelle côtés les facteurs d’un produit. On compte par fractions – définies, s’entend – en cherchant le rapport du nombre entier entre deux lignes. Ce qui rend justement la représentation du nombre zéro impossible, puisqu’il n’a aucun sens géométrique.
N’allez pas objecter, selon les habitudes de notre pensée différemment constituée que ceci est précisément le degré « primitif » de « la » mathématique en général. Dans le cadre de l’univers que l’homme antique s’était crée autour de soi, la mathématique antique est quelque chose d’achevé. Elle n’est imparfaite que pour nous. Les mathématiciens de Babylone et de l’Inde avait fait depuis longtemps ce qui était insensé pour le sentiment antique du nombre les parties essentielles de leurs mathématiques, et maint penseur grec le savait. « La » mathématique, nous ne cesserons de le répéter, est une illusion. Une pensée mathématique et, en général, scientifique est juste, convaincante, « logiquement nécessaire », quand elle répond entièrement au sentiment de la vie de ses auteurs. Sinon, elle est impossible, avortée, insensée ou, selon le mot favori de notre orgueil d’esprit historique, « primitive ». La mathématique moderne, chef d’œuvre de l’esprit occidental – « vraie » en tout cas pour lui seul – eut paru à Platon comme une méthode aberrante et ridicule pour se rapprocher de la vraie, entendez de l’antique mathématique ; il est certain que nous nous faisons à peine une idée de tout ce que nous avons laissé périr des grandes pensées des cultures étrangères, par ce que les bornes de notre pensée ne nous permettaient pas de nous les assimiler, ou, ce qui revient au même, par ce que nous avons senti qu’elles étaient fausses, superflues, insensées. »

Spengler, Le déclin de l’occident, première partie, chapitre I, § 5